《电机与拖动基础》课程知识速览

 

1 磁路※

  • 前情提要：
    • 电机是进行机电能量转换的装置
    • 机电能量转换的媒介是磁场，磁场的路径称为磁路
    • 在工程中，通常将磁场问题简化为磁路问题

1.1 磁路的基本定律※

1.1.1 磁场的几个常用物理量※

  • 磁感应强度（又称磁通密度）\(B\)
    • 表征磁场强弱及方向的物理量，它是一个矢量，单位：\(T\)（特斯拉）、\(1T=1Wb/m^2\)
    • 磁场中各点的磁感应强度可以用闭合的磁感应矢量线（磁力线）来表示
    • 磁力线与产生它的电流方向可以用右手螺旋定则来确定
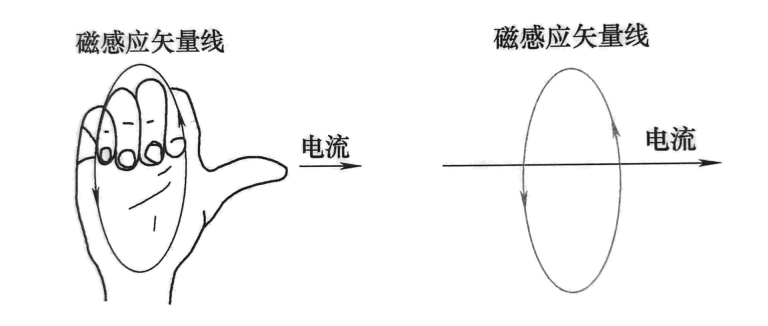
  • 磁通量 \(\phi\)
    • 垂直穿过某截面积的磁力线总和，标量，单位：\(Wb\)（韦伯）
    • 在均匀磁场中，磁感应强度 \(B\) 与垂直于磁场方向面积 \(A\) 的乘积，为通过该面积的磁通量，称为磁通量，简称磁通 \(\phi\) 
    • \(𝐵 = \phi /𝐴\)
  • 磁场强度 \(H\)
    • 计算磁场时引用的物理量，矢量
    • 描述磁场源的特性，与介质无关的物理量
    •  \(B=\mu H\)，单位：\(A/m\)
    •  \(\mu\)：用来表示物质磁导能力大小的量称为磁导率
    • 真空的磁导率 \(\mu_0 = 4\pi \times 10^{-7}H/m\)
    • 铁磁材料的磁导率 \(\mu_{Fe} >> \mu_0\)

1.1.2 磁路的概念※

  • 定义：如同把电流流过的路径称为电路一样，磁通所通过的路径称为磁路。
  • 补充：
    • 主磁通和漏磁通所通过的路径分别构成主磁路和漏磁路，例如直流电机的磁路。
    • 励磁电流为直流的叫做直流磁路，励磁电流为交流的叫做交流磁路，例如交流铁心线圈、变压器、感应电机的磁路。

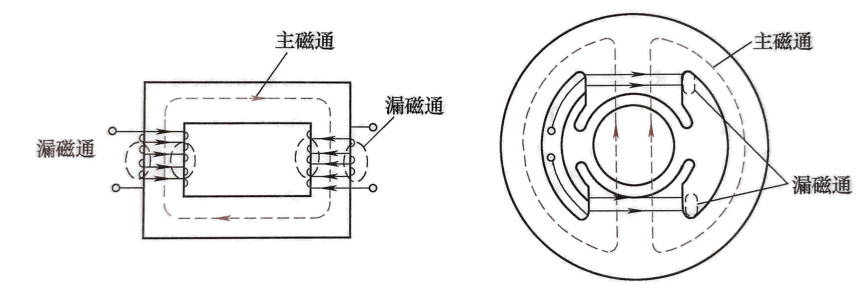
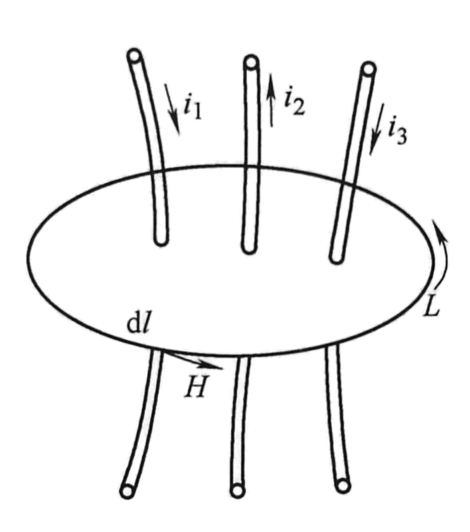
1.1.3 磁路的基本定律※

  • 安培环路定律
    • 沿任何一条闭合回线 \(L\) ，磁场强度 \(H\) 的线积分等于该闭合回线所包围的电流的代数和 \(\oint_{L} Hdl = \sum i\) 
    • 沿着回线 \(L\) ，磁场强度 \(H\) 处处相等（均匀磁场），且闭合回线所包围的总电流是由通有电流 \(i\) 的 \(N\) 匝线圈所提供，则公式可简化为 \(Hl = Ni\)
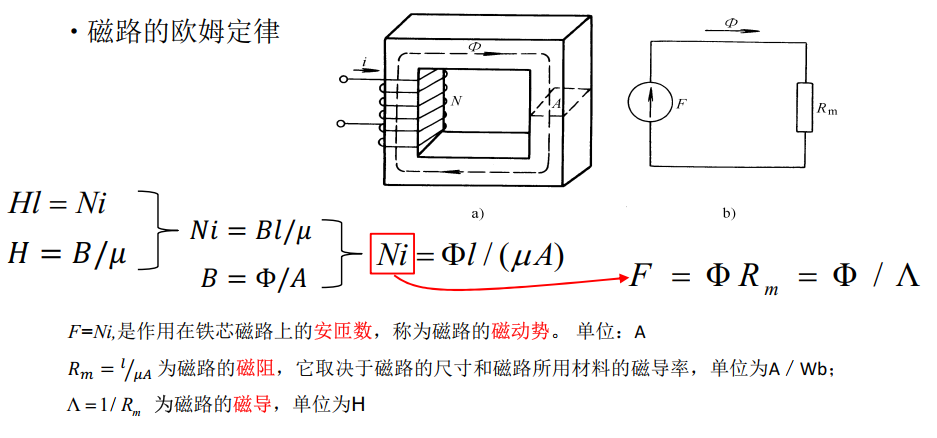
  • 磁路的欧姆定律
    • 公式 \(\phi = F / R_m\)
    • 磁动势 \(F\) ，\(F = NI\) ，单位安匝（At）
    • 磁阻 \(R_m\)，\(R_m = I / (\mu A)\)，单位 \(H^{-1}\) 或 \(At/Wb\)

 

  • 磁路的基尔霍夫定律
    • 磁路的基尔霍夫电流定律：\(\sum \phi\)
    • 磁路的基尔霍夫电压定律：\(\sum F = \sum Hl = \sum \phi R_m\)
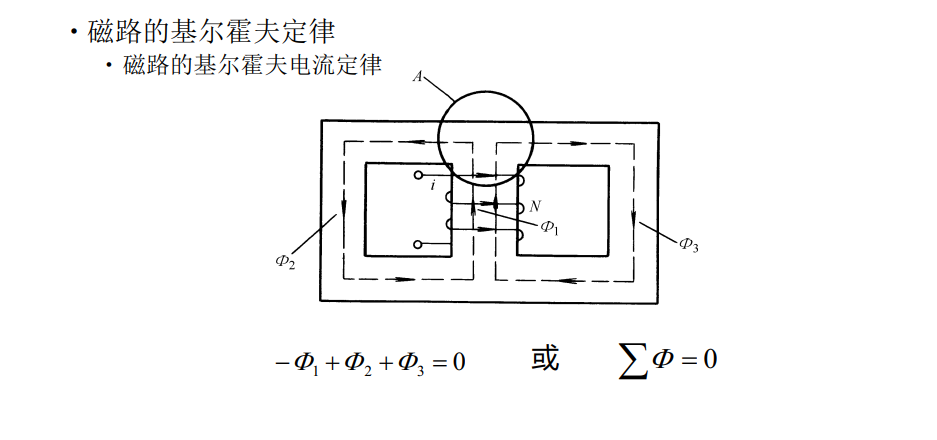
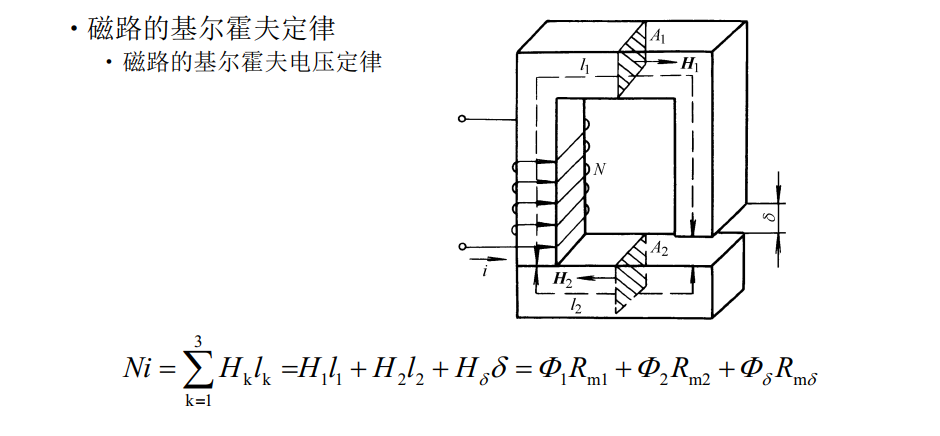
  • 磁路和电路有相似之处，却要注意有以下几点差别：
    • 电路中有电流 \(I\) 时，就有功率损耗 \(I^2R\) ；而在直流磁路中，维持一定磁通量 \(\phi\)，铁心中没有功率损耗。
    • 电路中的电流全部在导线中流动；而在磁路中，总有一部分漏磁通。
    • 电路中导体的电阻率在一定的温度下是恒定的；而磁路中铁心的导磁率随着饱和程度而有所变化。
    • 对于线性电路，计算时可以用叠加原理；而在磁路中，\(B\) 和 \(H\) 之间的关系为非线性，因此计算时不可以用叠加原理。

>>> 磁路与电路仅为形式上的类似 <<<

1.2 常用的铁磁材料及其特性※

（1）铁磁物质的磁化

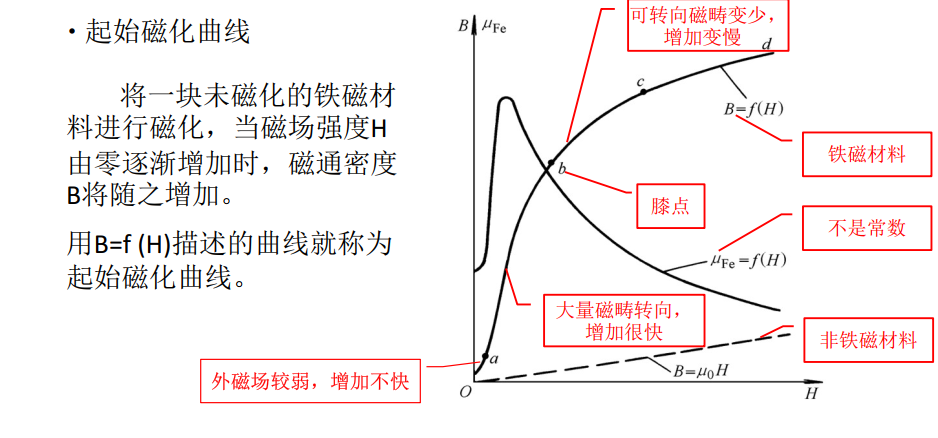
铁磁物质包括铁、镍、钴等以及它们的合金。将这些材料放入磁场中，磁场会显著增强。铁磁材料在外磁场中呈现出很强的磁性，此现象称为铁磁物质的磁化。铁磁物质能被磁化的原因是在它内部存在着许多很小的被称为磁畴的天然磁化区。磁畴用一些小磁铁来示意表明。在没有外磁场的作用时，各个磁畴排列混乱，磁效应互相抵消，对外不显示磁性。在外磁场的作用下，磁畴就顺外磁场方向而转向，排列整齐并显示出磁性来。这就是说铁磁物质被磁化了。由此形成的磁化磁场，叠加在外磁场上，使合成磁场大为加强。

非铁磁材料的磁导率接近于真空的磁导率 \(\mu_0\) ，电机中常用的铁磁材料磁导率 \(\mu_{Fe} = (2000 \thicksim 6000)\mu_0\) 

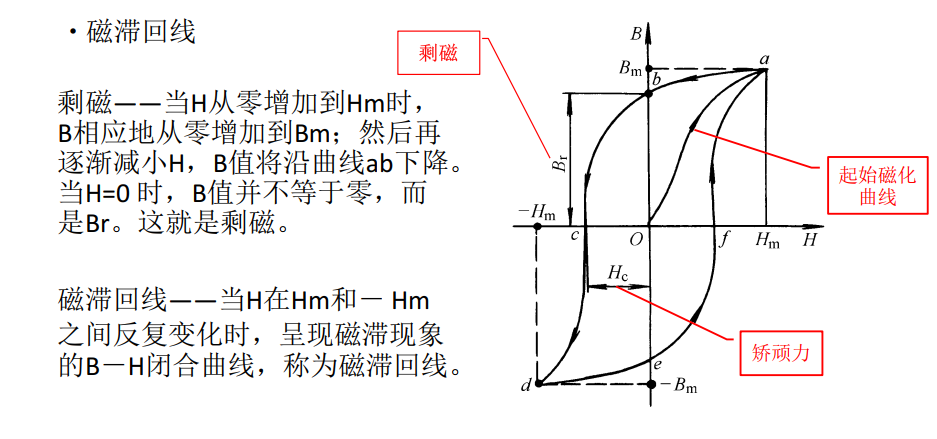
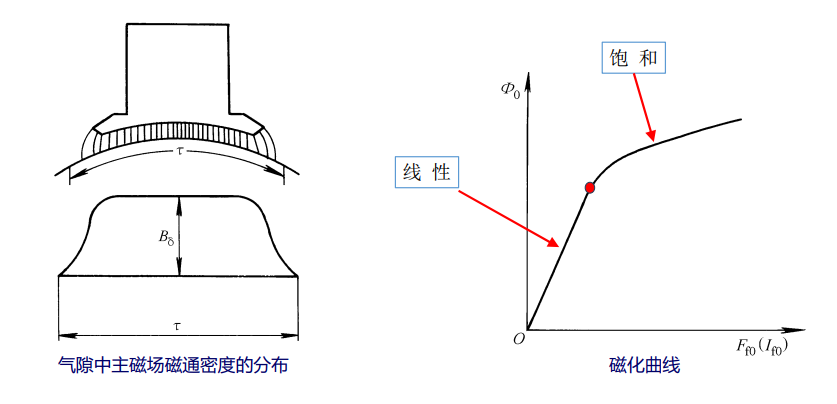
（2）磁化曲线和磁滞回线

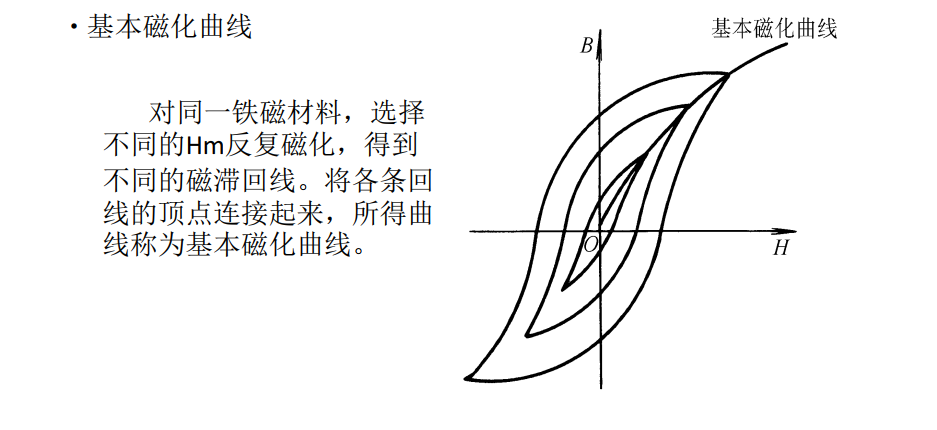
（3）铁磁材料

  • 软磁材料
    • 磁滞回线较窄，剩磁和矫顽力都小
  • 硬磁材料
    • 磁滞回线较宽，剩磁和矫顽力都大

（4）铁心损耗

2 直流电机※

2.1 直流电机的工作原理※

（1）直流电动机的工作原理

直流电动机的工作原理是建立在安培定律的基础上的。这里先回顾一下安培定律。

根据实验可知，若磁场与载流导体互相垂直（见图2-1a），作用在该导体上的电磁力为

\[F=BIL\]
  • 磁感应强度 \(B\) 的单位为 \(\text{Wb/m}^2\)（特斯拉，\(T\)）
  • 导体中的电流 \(I\) 单位为 \(\text{A}\)
  • 导体的有效长度 \(L\) 单位为 \(\text{m}\)

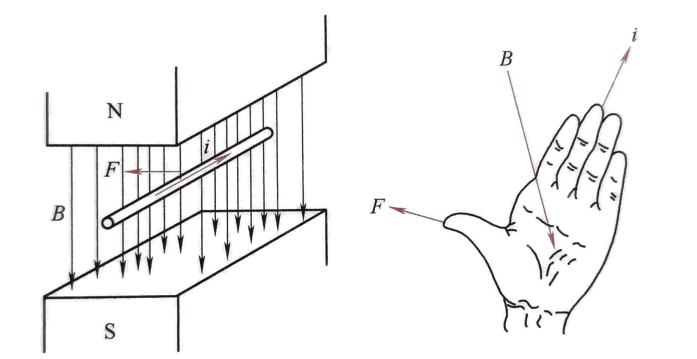
当线圈ax中通入直流电流时，线圈边a和x上均受到电磁力，根据左手定则确定力的方向。这一对电磁力形成了作用于电枢的一个电磁转矩。

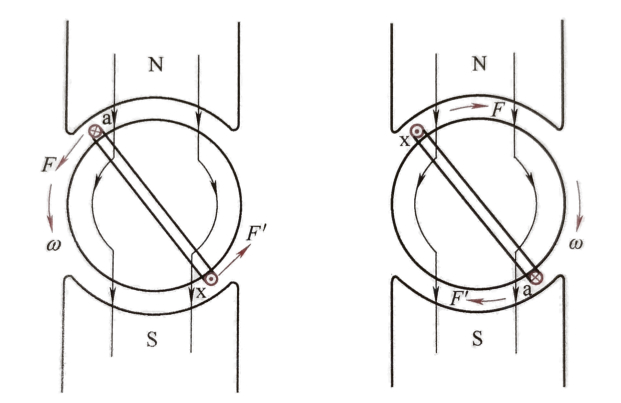
换向器配合电刷对电流的换向作用，线圈边只要处在N极下，电流总是由电刷A流入；线圈边在S极下时，电流总是从电刷B流出，使电动机能连续旋转（逆时针转矩），旋转后负载类型有变化：线圈两端感应出反电动势
 

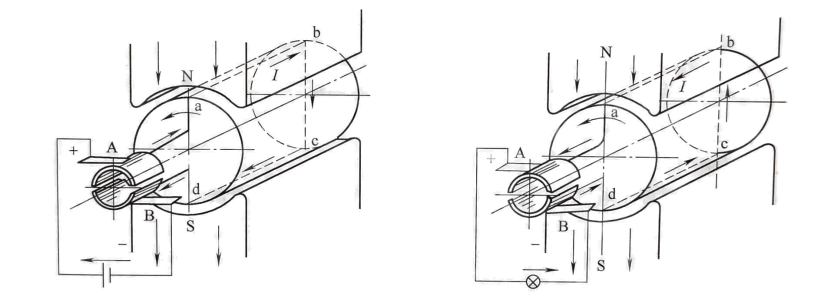
（2）直流发电机的工作原理

如上图所示，用原动机拖动电枢逆时针方向恒速转动，线圈边ab和cd就分别切割不同极性磁极下的磁场，线圈中产生了交变的电动势，由于换向器配合电刷对电流的换向作用，在电刷A、B端的电动势是直流电动势 

2.2 直流电机的结构※

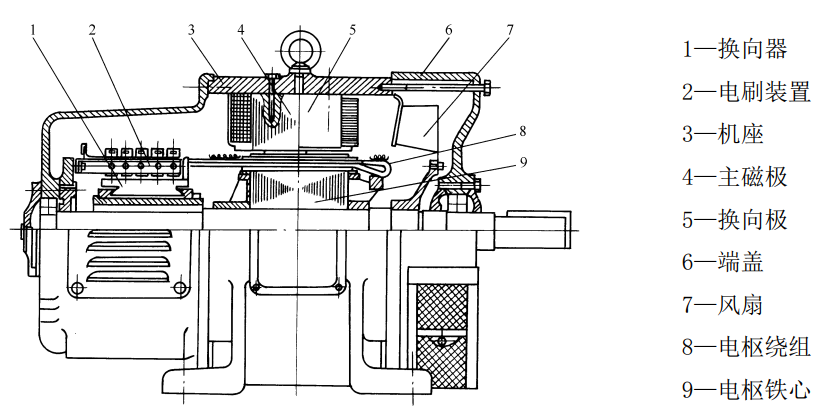
▶️ 视频讲解：《上课没弄懂，打算给老师上一课！3D演示直流电机的设计思路和原理》

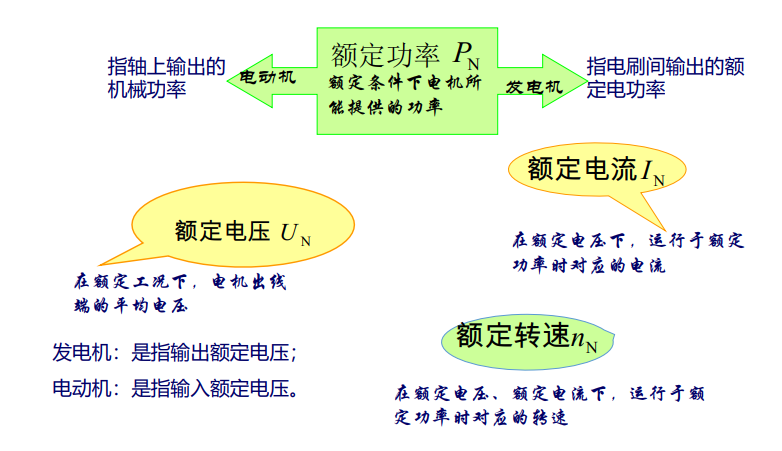
2.3 直流电机的铭牌数据※

直流电机的额定值有：

  1. 额定功率 \(P_N\) (kW)
  2. 额定电压 \(U_N\) (V)
  3. 额定电流 \(I_N\) (A)
  4. 额定转速 \(n_N\) (r/min)
  5. 额定励磁电压 \(U_{fN}\) (V) 

2.4 直流电机的绕组※

2.4.1 简单绕组※

 

2.4.2 单叠绕组※

 

2.4.3 单波绕组※

 

2.5 直流电机的励磁方式※

  • 他励
  • 串励
  • 并励
  • 复励

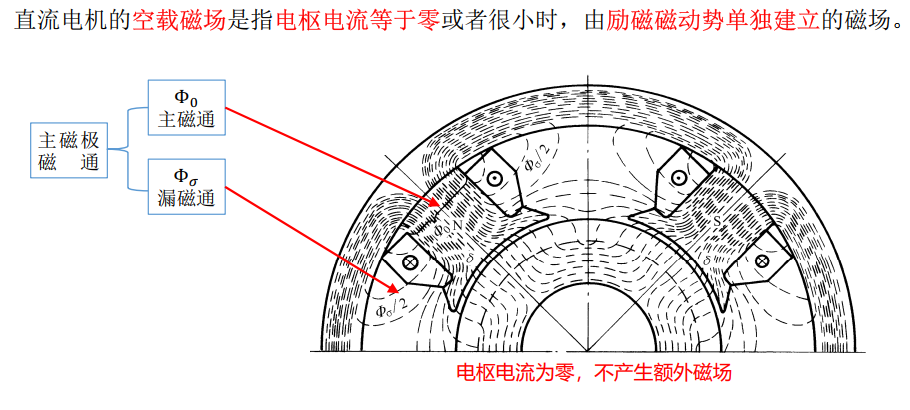
2.6 直流电机的空载磁场※

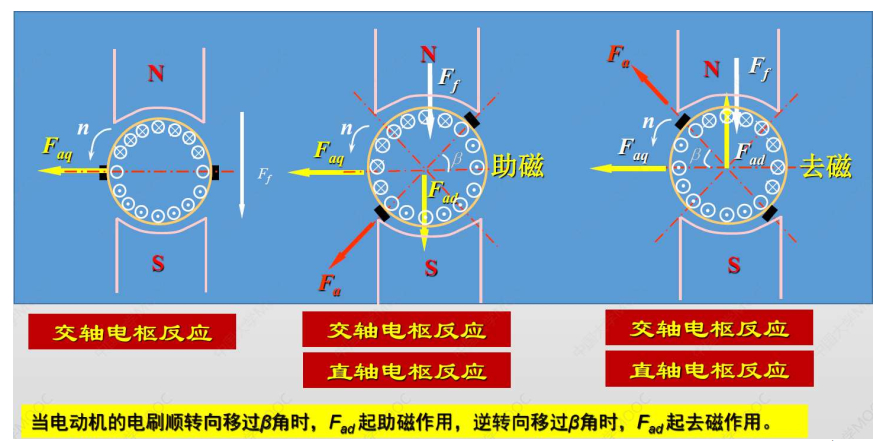
2.7 直流电机负载时的磁场及电枢反应※

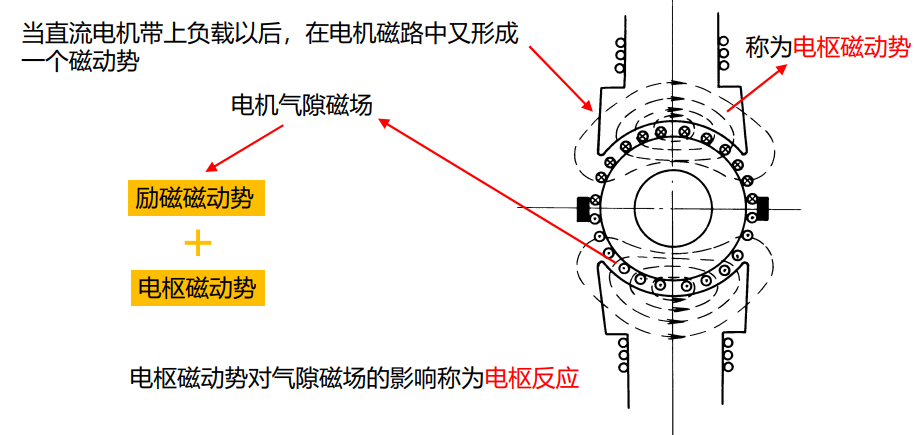
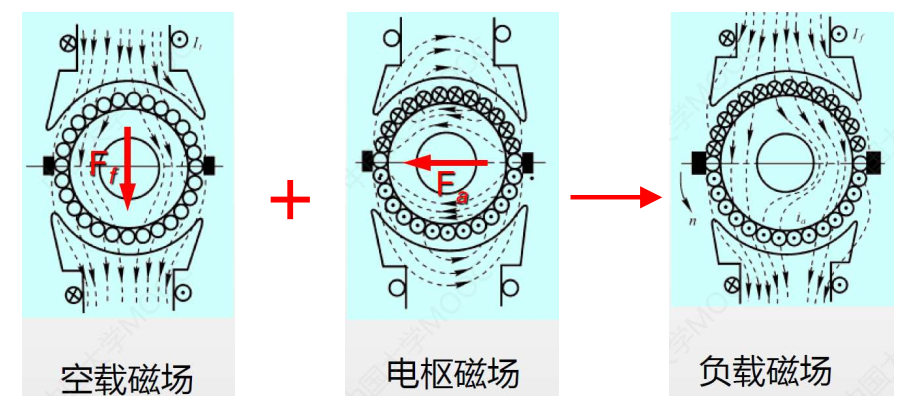
励磁绕组 + 电枢绕组 + 串励绕组 + 换向绕组

2.8 感应电动势和电磁转矩的计算※

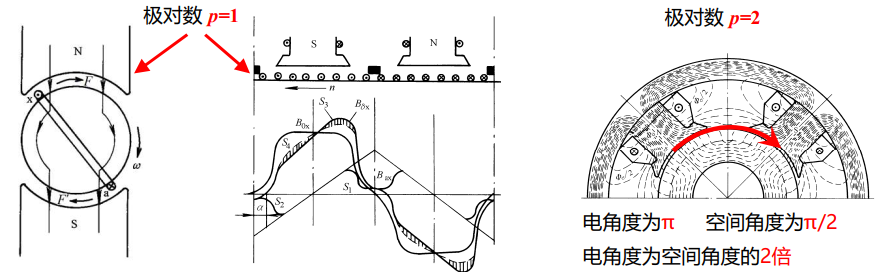
2.8.1 基础概念与极对数※

  • 极对数 (\(p\)):
    • 当 \(p=1\) 时，电角度与空间角度相同。
    • 当 \(p=2\) 时，电角度为空间角度的2倍。
    • 结论: 电角度 = \(p \times\) 空间角度。
  • 转速 (\(n\)): 电枢在空间中的旋转速度，单位：\(r/min\)。
  • 电角速度 (\(\omega\)): 电枢以电角度为单位的旋转速度，单位：\(rad/s\)。
    • 计算公式: \(\omega = \frac{p \times n \times 2\pi}{60}\)

2.8.2 感应电动势※

  • 时间计算: 电枢转过 \(\pi\) 电角度（即一个极距）所需的时间 \(\Delta t\): 
\[\Delta t = \frac{\pi}{\omega} = \frac{\pi}{\frac{2p\pi n}{60}} = \frac{60}{2pn}\]
  • 平均感应电动势: 根据电磁感应定律，一个匝数为 \(N_y\) 的元件中感应电动势的平均值为: 
\[E_{avg} = 4N_{y}\frac{pn}{60}\Phi\]
  • 对于整个电枢绕组，设总有效导体数为 \(Z\)，支路数为 \(a\) (总电流 \(I_a\) 分为 \(2a\) 个支路，但此处 \(a\)通常指支路对数或直接指支路数，根据讲义 \(C_e\) 定义推断):
\[E_{a} = \frac{pZ}{60a}\Phi n = C_{e}\Phi n\]
  • 电动势常数 \(C_{e} = \frac{pZ}{60a}\)
    • 对于制成的电机，\(C_e\) 为常数。
  • 支路数 (\(a\)) 取值:
    • 单叠绕组: \(a=p\)
    • 单波绕组: \(a=1\) (注：通常指并联支路对数或相应定义，此处依据课件原文 \(a=1\))
  • 若不计饱和影响，磁通 \(\Phi\) 与励磁电流 \(I_f\) 成正比 (\(\Phi = K_f I_f\))，则: \(E_{a} = C_{e}K_{f}I_{f}n = G_{af}I_{f}\Omega\)
    • 其中 \(\Omega\) 为机械角速度。
    • 系数 \(G_{af} = C_T K_f\)。

2.8.3 电磁转矩※

直流电机的电磁转矩 \(T_e\) 由气隙磁通 \(\Phi\) 和电枢电流 \(I_a\) 共同作用产生:

\[T_{e} = \frac{pZ}{2\pi a}\Phi I_{a} = C_{T}\Phi I_{a}\]\[C_{T} = \frac{pZ}{2\pi a}\]\[C_{T} = 9.55 C_{e}\]

 (注: 来源由 \(60 / 2\pi \approx 9.55\) 推导得出)

电磁功率、感应电动势与电磁转矩之间存在如下平衡关系:

\[E_{a}I_{a} = T_{e}\Omega\]

 (亦可表示为 \(G_{af}I_{f}\Omega I_{a} = T_{e}\Omega\))

  • 电动机运行:
    • 从电源获取电磁功率 \(E_{a}I_{a}\) \(\rightarrow\) 电磁转矩对机械负载做功 \(T_{e}\Omega\)（输出机械功率）。
  • 发电机运行:
    • 原动机克服电磁转矩做功 \(T_{e}\Omega\)（输入机械功率）\(\rightarrow\) 发出电磁功率 \(E_{a}I_{a}\)。

2.9 直流电机的运行原理※

2.9.1 直流电机的基本方程式※

（1）电动势平衡方程式(并励电动机)

\[u_a = G_{af}i_f \Omega+ R_a i_a + L_a \frac{di_a}{dt}\]\[u_f = R_f i_f + L_f \frac{di_f}{dt}\]\[u_a = u_f = u\]

式中

  • \(u\) —— 电源电压；
  • \(u_a\) —— 电枢绕组上的端电压；
  • \(u_f\) —— 励磁绕组上的端电压；
  • \(i_a\) —— 电枢电流；
  • \(i_f\) —— 励磁电流；
  • \(R_a\) —— 电枢电路的电阻（其中包括电刷与换向器的接触电阻）；
  • \(R_f\) —— 励磁回路的电阻；
  • \(L_a\) —— 电枢回路的自感系数；
  • \(L_f\) —— 励磁回路的自感系数；
  • \(\Omega\) —— 电动机的机械角速度。

 

 

 

3 变压器※

 

4 异步电机（一）※

 

5 异步电机（二）※

 

8 电机拖动系统动力学基础※

 

9 直流电动机的电力拖动※

 

 

“您的支持是我持续分享的动力”

微信收款码
微信
支付宝收款码
支付宝
目录